04. Vectors- Mathematical definition
Vectors- Mathematical Definition
What is a Vector? The plain explanation would be that a vector is an ordered list of numbers.
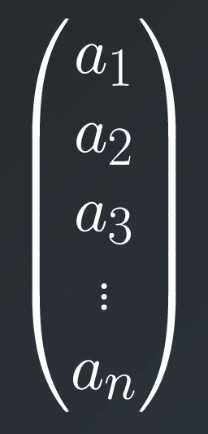
n Dimensional Vector
Each element in the vector, also called component or coordinate, is a number, denoted here by a_i.
This specific vector (in the picture above ) has n elements and can be in the field of Real Numbers \mathbb{R}.
A vector of n real elements defines an n dimensional vector and belongs to \mathbb{R}^n.
We use the following mathematical notation to define a vector: \vec{x}
In the example above:
\vec{x}\in\mathbb{R}^n
\vec{x}=\begin{bmatrix} x_1\\ x_2\\ x_3\\ :\\x_n\end{bmatrix}
As in the video let’s put this into a more visual context and focus on a 2D vector of the field of real numbers. In other words, we will focus on a vector in \mathbb{R}^2, which defines all points on the plane.
Lets look at the following picture:
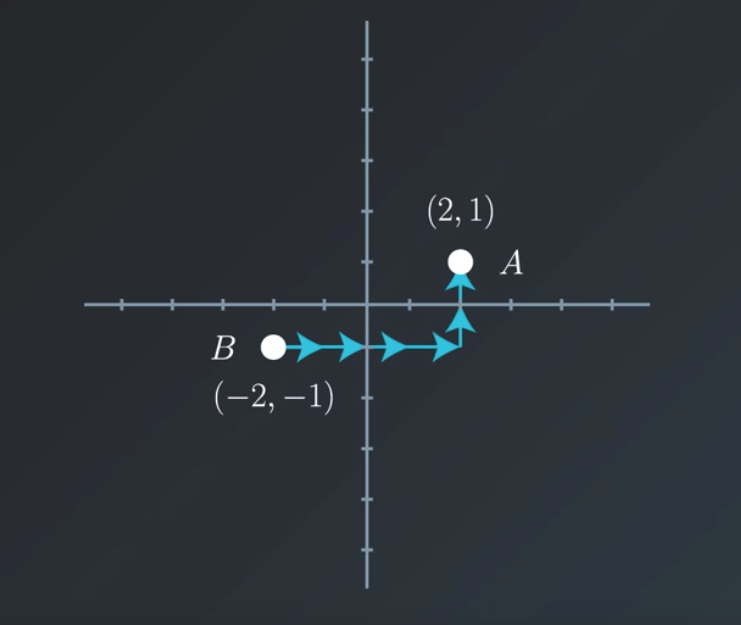
To go from point B to point A we will need to take 4 steps to the right and 2 steps up.
This defines the vector \vec{x}=\begin{bmatrix} 4\\2\end{bmatrix}.
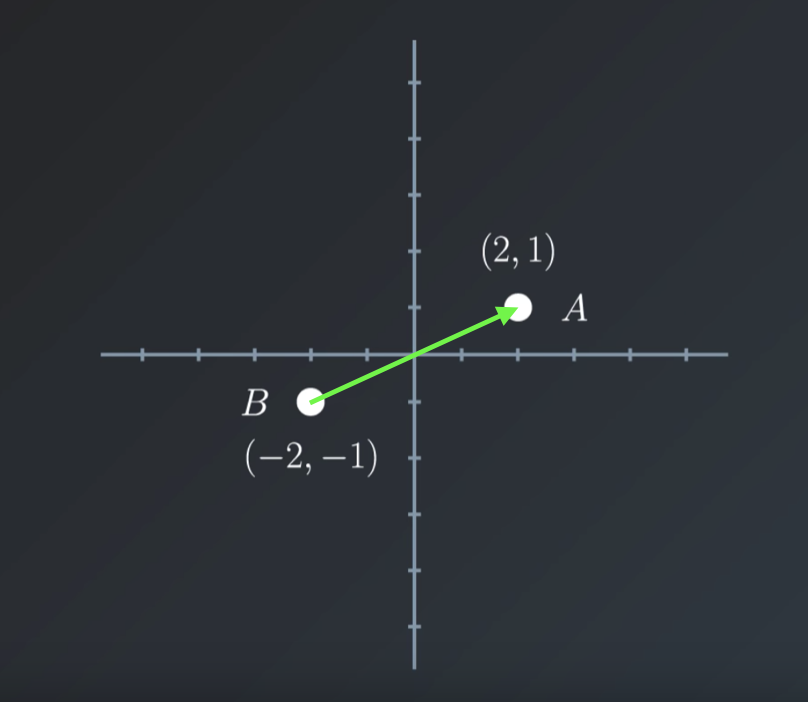
The green arrow below defines vector \vec{x}.
Graphically we use an arrow to illustrate a vector, as depicted in the following picture.
To calculate the direction of the movement we will use an angle. We can use Degrees or Radians. In this example we will focus on Degree. (It is always possible to move Degrees to Radians and vice versa).